Proyeksi Vektor: Konsep, Rumus, dan Aplikasinya dalam Matematika

Dalam matematika dan fisika, proyeksi vektor adalah konsep penting yang digunakan dalam berbagai bidang, seperti analisis vektor, fisika, dan pemrograman grafis. Artikel ini akan membahas secara mendalam mengenai proyeksi vektor, mulai dari definisi, rumus-rumus utama, hingga aplikasinya dalam kehidupan nyata.

Pengertian Proyeksi Vektor

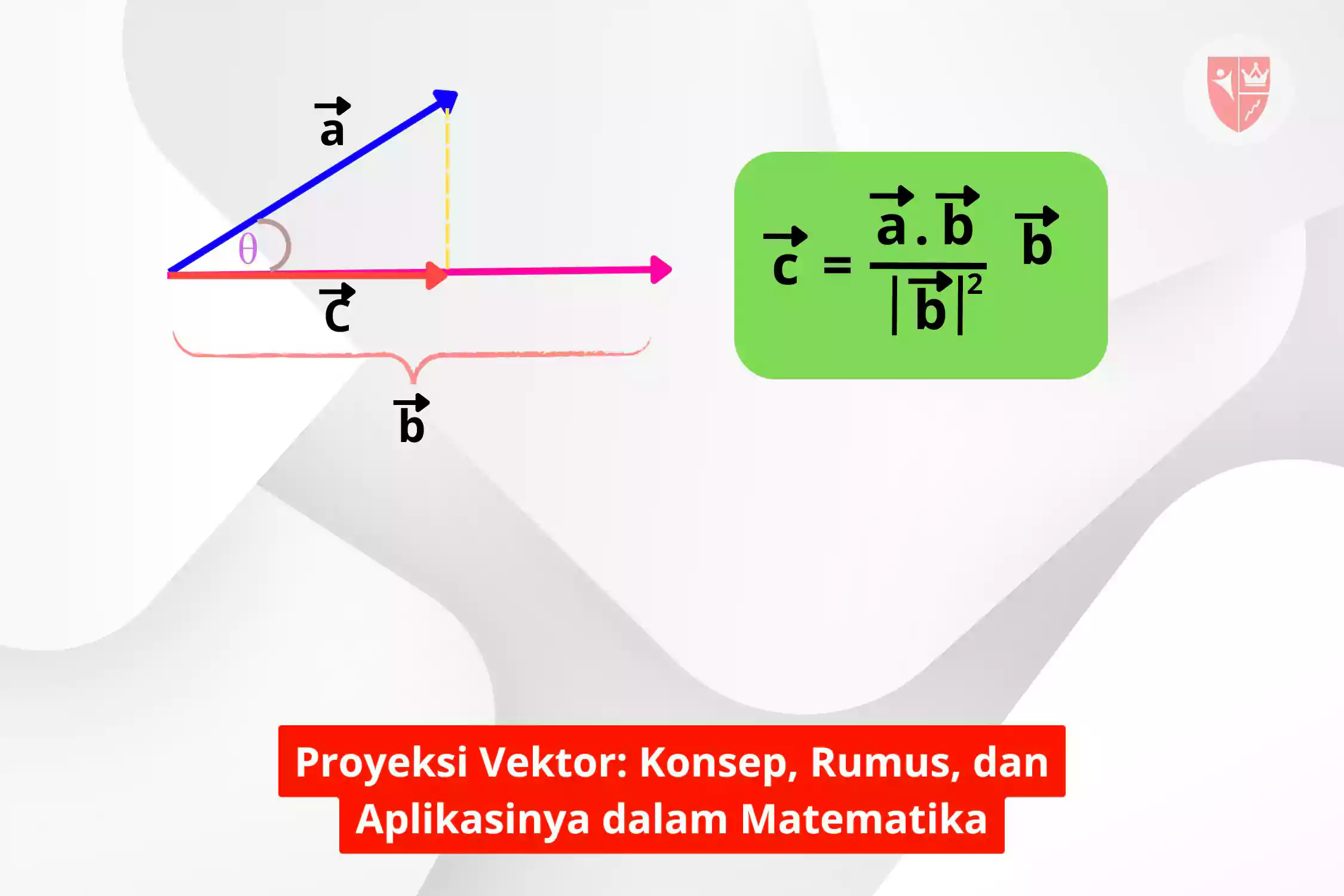
Proyeksi vektor adalah representasi satu vektor pada vektor lainnya. Dengan kata lain, proyeksi vektor dari $latex \displaystyle \overrightarrow{a}$ pada $latex \displaystyle \overrightarrow{b}$ adalah bayangan vektor $latex \displaystyle \overrightarrow{a}$ jika dilihat dari arah $latex \displaystyle \overrightarrow{b}$.

Secara umum, terdapat dua jenis proyeksi vektor:

1. Proyeksi Skalar – Menghasilkan skalar yang menunjukkan panjang proyeksi vektor pertama pada vektor kedua.
2. Proyeksi Vektor – Menghasilkan vektor yang sejajar dengan vektor kedua.

Rumus Proyeksi Vektor

Untuk dua vektor $latex \displaystyle \overrightarrow{a}$ dan $latex \displaystyle \overrightarrow{b}$ dalam ruang Euclidean, proyeksi skalar dan proyeksi vektor dihitung dengan rumus berikut:

Proyeksi Skalar

Proyeksi skalar dari $latex \displaystyle \overrightarrow{a}$ pada $latex \displaystyle \overrightarrow{b}$ diberikan oleh:

$latex \displaystyle pro{{j}_{b}}\left( a \right)=\frac{{\overrightarrow{a}.\overrightarrow{b}}}{{\left| b \right|}}$

Di mana:

• $latex \displaystyle \overrightarrow{a} \cdot \overrightarrow{b}$ adalah hasil dot product dari vektor $latex \displaystyle \overrightarrow{a}$ dan $latex \displaystyle \overrightarrow{b}$,
• $latex \displaystyle |\overrightarrow{b}|$ adalah norma (panjang) vektor $latex \displaystyle \overrightarrow{b}$.

Proyeksi Vektor

Proyeksi vektor dari $latex \displaystyle \overrightarrow{a}$ pada $latex \displaystyle \overrightarrow{b}$ dihitung dengan rumus:

$latex \displaystyle pro{{j}_{{\overrightarrow{b}}}}\left( {\overrightarrow{a}} \right)=\frac{{\overrightarrow{a}.\overrightarrow{b}}}{{{{{\left| b \right|}}^{2}}}}\overrightarrow{b}$

Contoh Perhitungan

Misalkan terdapat dua vektor dalam ruang dua dimensi:

$latex \displaystyle \overrightarrow{a}=\left( {3,4} \right)$, $latex \displaystyle \overrightarrow{b}=\left( {1,2} \right)$

Langkah-langkah menghitung proyeksi vektor $latex \displaystyle \overrightarrow{a}$ pada $latex \displaystyle \overrightarrow{b}$ adalah sebagai berikut:

1. Hitung Dot Product $latex \displaystyle \begin{array}{l}\overrightarrow{a}.\overrightarrow{b}=\left( {3\times 1} \right)+\left( {4\times 2} \right)\\\overrightarrow{a}.\overrightarrow{b}=3+8\\\overrightarrow{a}.\overrightarrow{b}=11\end{array}$
2. Hitung Norma Vektor$latex \displaystyle \left| {\overrightarrow{b}} \right|=\sqrt{{{{1}^{2}}+{{2}^{2}}}}=\sqrt{5}$
3. Hitung Proyeksi Skalar $latex \displaystyle pro{{j}_{b}}\left( a \right)=\frac{{11}}{{\sqrt{5}}}$
4. Hitung Proyeksi Vektor $latex \displaystyle pro{{j}_{{\overrightarrow{b}}}}\left( {\overrightarrow{a}} \right)=\frac{{11}}{5}\left( {\begin{array}{*{20}{c}} 1 \\ 2 \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {\frac{{11}}{5}} \\ {\frac{{22}}{5}} \end{array}} \right)$

Aplikasi Proyeksi Vektor

1. Fisika

Dalam mekanika, proyeksi vektor digunakan untuk menghitung komponen gaya sepanjang sumbu tertentu.

2. Pemrograman Grafis

Proyeksi vektor digunakan dalam rendering 3D untuk memproyeksikan objek ke layar 2D.

3. Machine Learning

Dalam analisis data, proyeksi digunakan untuk reduksi dimensi seperti PCA (Principal Component Analysis).

Proyeksi vektor adalah konsep fundamental dalam matematika yang memiliki banyak aplikasi dalam berbagai bidang. Dengan memahami proyeksi skalar dan proyeksi vektor, kita dapat menerapkannya dalam berbagai permasalahan nyata, seperti fisika, pemrograman, dan analisis data.

Dengan artikel ini, diharapkan pemahaman mengenai proyeksi vektor menjadi lebih jelas dan aplikatif.